Making a Simple Exhaust Pipe Jog

So, recently I was working on an exhaust project.  I needed a 1-3/4" exhaust pipe to make a 2" jog.  The two legs of the jog needed to be parallel, and, because of the tight area, I needed to get the jog done in the minimum of space.  I first fiddled with some trial and error attempts, but finally decided to throw a little math at the problem.  I found that the puzzle could be simplified by realizing that all we really need to look at is the pipe center lines.  If the pipe center line jogs two inches, the pipe jogs two inches. 

One good way to accomplish a jog like this is to use two straight pipes, each with a bend arc at the end.  If the bend arcs are identical, we have something like in this image below.  As the image implies, the centerline of the jog stays in one plane.





Having the pieces identical guarantees that the inlet and outlet pipes are parallel, since what one arc does, the other un-does.  Also, it's important that the arc cuts be along a radius of the bends.  This makes a cut "square" cut to the centerline, which guarantees that the open end is a circle, and not an ellipse.

So, the two variables we have to work with are the radius of the bend  (AB or AC in the figure above), and how much of the bend we use (the angle Θ in the figure).  The amount the centerline deviates from the centerline of the straight section of pipe on each side is labeled h, so the total jog (Jog Rise) is 2h.  The distance required to make the jog is the Jog Run (2 x DC in the figure).

Since AC is the bend radius, r, we see that
DC = r·sinΘ,
which is half of the Jog Run, so
Jog Run = 2r·sinΘ.


Likewise, since

AD = r·cosΘ,
h = AB-AD
= r - r·cosΘ
=r(1- cosΘ), 

Which is half of the Jog Rise, so

Jog Rise = 2r(1 - cosΘ).

Now, here is where we have to get more specific.  We need to pick a bend radius.  For my purposes, I needed to minimize the Jog Run, so that means making r as small as possible.  However, there is a limit to how tight a bend we can get in a given size of pipe.  The smallest bend radius I was able to find was equal to the pipe diameter, so for my 1.75" OD pipe jog, I ordered a couple of 180 degree mandrel bends in 1.75 OD pipe, with a 1.75" bend radius.

So, with r known, I had to determine how much of the bend to use for each half of the jog.  A little algebra on the Jog Rise formula, solving for Θ, we get
Θ = arccos(1-Jog Rise/2r).
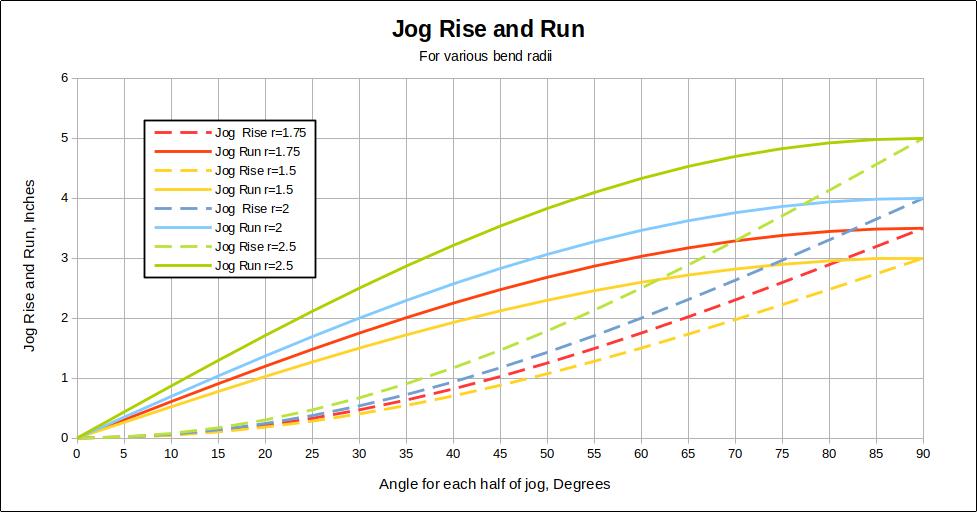
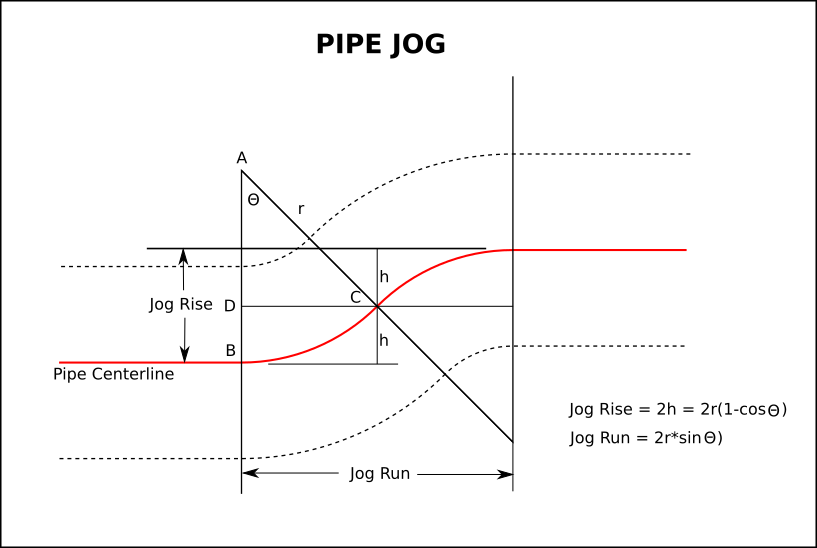
That angle then can be plugged into the Jog Run formula to find the Jog Run.
Or, if those sin and arccos things seem a little intimidating, use the chart below.  To use the chart, pick the desired Jog Rise on the vertical axis.  Follow horizontally to the dotted Jog Rise curve corresponding to the bend radius.  Then drop down to find the angle of arc for each half of the jog.  From that point, go vertically up to the solid Jog Run line for the bend radius, then back to the left to read the Jog Run.